Wer sich ernsthaft mit dem Thema Optionen beschäftigt, stößt irgendwann unweigerlich auf die sogenannten Griechen beim Optionshandel. Doch was hat es mit dem Delta, dem Gamma, dem Theta und dem Vega auf sich und muss ich das wirklich alles wissen? Genau das besprechen wir heute in diesem Artikel.
Eines möchte ich an dieser Stelle vorwegnehmen, das Verständnis des Inhalts dieses Artikels ist nicht zwingend erforderlich, um Optionen zu handeln und speziell die im Optionshandel ABC vorgestellten Stillhaltergeschäfte zu betreiben. Es hilft aber ggf. die Zusammenhänge besser zu verstehen, wenn man auch die Hintergründe dazu kennt.
Ich selbst beschäftige mich seit nunmehr fast 5 Jahren mit dem Thema Optionen und benutze die Griechen wirklich nur am Rande. Ich bin gerade am Anfang komplett ohne dieses Wissen klargekommen und das wäre dann auch direkt meine erste Empfehlung. Wer erstmalig mit dem Optionshandel beginnen möchte, der muss das hier nicht gleich verstehen wollen.
Fangt erst mal an. Just do it! Macht ein paar kleine Trades und schaut dann wieder hier rein, okay?
Der Anfang ist die Hälfte des Ganzen.
Gut gut. Und damit ohne weiteres Vorgeplänkel, legen wir los.
Bisher haben wir im Rahmen des Optionshandel ABC beleuchtet:
- Teil 1: Grundlagen vor dem Start
- Teil 2: Was sind Stillhaltergeschäfte?
- Teil 3: Der Cash Secured Put
- Teil 4: Der Covered Call
- Teil 5: Das Rollen von Optionen
- Teil 6: Optionshandel oder Dividendenstrategie?
- Teil 7: Der beste Broker für den Optionshandel
- Teil 8: Optionen schreiben in der Praxis
- Bonus: Die 50% Regel – Gewinne absichern!
- Bonus: 5 Jahre mit der Wheel-Strategie
Und heute kommt ein neuer Teil hinzu:
- Bonus: Die Griechen beim Optionshandel

Was haben die Griechen damit zu tun?
Die Griechen haben ja sehr viele Dinge erfunden, die bis heute ein wichtiger Teil unserer Gesellschaft sind. Die Demokratie vielleicht, nur um ein kleines Beispiel zu nennen? Da die Börse und der Optionshandel in der jetzigen Form aber eine Erfindung der Neuzeit sind, haben die alten Griechen hier mal ausnahmsweise nicht ihre Finger im Spiel.
Die Bezeichnung Die Griechen (Greeks) leitet sich dagegen ganz einfach aus der Tatsache ab, dass bestimmte Parameter in den Optionspreismodellen (Black-Schole-Modell) als Abkürzung griechische Buchstaben tragen. Wenn wir also beim Optionshandel von den Griechen sprechen, dann sind damit Variablen in einer mathematischen Gleichung gemeint. Nicht mehr und nicht weniger.
Oh je! Mathematische Gleichung? An der Stelle hab ich bestimmt 50% der Leser verloren, oder? 😉
Aber keine Angst, hier gibt es keine Matheaufgaben zu lösen. Wir besprechen diese Variablen nur, um ein besseres Verständnis der Hintergründe zu bekommen, wie sich zum Beispiel Optionspreise über die Laufzeit entwicklen können. Dabei geht es nicht um exakte Berechnungen eines Preises oder einer Preisentwicklung. Das übersteigt auch meine Fähigkeiten und ist meiner Meinung nach in der Praxis nicht relevant.
Und es ist auch nicht nötig, denn das hier erworbene Verständnis kann man immer noch hervorragend dafür nutzen, um zum Beispiel einfach mal 2 Optionen miteinander zu vergleichen. Dazu versuche ich in den nachfolgenden Abschnitten, jeweils immer ein leicht verständliches Beispiel zu geben.
Anmerkung: Ich schreibe im Artikel allgemein von Optionen, meine dabei aber immer explizit nur Aktienoptionen. Ich selbst handle keine Futures oder andere Optionskonstrukte, einzig einfache Call & Put Optionen auf Aktien (vorzugsweise Dividendenaktien) sind Teil meiner Strategie.
Das Delta

Definition: Das Delta ist eine Sensitivitätskennzahl, die angibt, welchen Einfluss der Preis des Basiswerts auf den Wert der Option hat. Das Delta ist mathematisch die erste Ableitung des Optionspreises nach dem Preis des Basiswerts. Ein Delta von 0,5 bzw. 50% bedeutet, dass eine Veränderung des Basiswerts um 1 EUR eine Veränderung des Optionspreises von 0,50 EUR hervorruft.
Als Faustregel kann man sich also schonmal merken: Je höher das Delta, desto stärker reagiert die Option auf Kursveränderungen des Basiswerts.
Das Delta kann dabei einen Wert zwischen +1 und -1 annehmen, wobei das Vorzeichen in der Regel weggelassen wird, da es sich auch aus der Optionsart (Call oder Put) ablesen lässt. Das Delta wird außerdem häufig in Prozent angegeben. Eine Darstellung von zum Beispiel 1 = 100% oder 0,5 = 50% ist demzufolge dasselbe.
Wenn die Option weitmöglichst aus dem Geld (out of the money) liegt, strebt diese tendenziell ein Delta von 0 (0%) an. Bei einem Delta von 0 (0%) gäbe es außerdem keine Korrelation mehr zwischen Option und Basiswert. Man sagt auch, die beiden Werte sind entkoppelt.
Liegt eine Option dagegen tiefstmöglich im Geld (in the money), so strebt diese tendenziell immer ein Delta von 1 (100%) an. Außerdem bedeutet ein Delta von 1 (100%), dass es eine absolute Korrelation gäbe. Die Option würde also jede Änderung des Basiswerts eins zu eins mitmachen.
In der Praxis erreicht man ein Delta von genau 0 (0%) oder 1 (100%) zwar nicht, aber man kann sich beliebig annähern. In der Regel liegt der Wert immer irgendwo dazwischen, wobei ein Delta von 0,5 (50%) ungefähr den Wert am Geld (at the money) darstellt.
Merke:
- Out of the money = Tendenz Delta 0 (0%)
- At the money = Tendenz Delta 0,5 (50%) bzw. -0,5 (-50%)
- In the money = Tendenz Delta 1 (100%) bzw. -1 (-100%)
Welche Möglichkeiten gibt es also?
Nehmen wir das Beispiel einer Aktie im Wert von 100 EUR und einer Option dazu im Wert von 2 EUR und dem Delta von 0,25 (25%) und du tritts als Käufer der Option in Aktion.
- Long Call = Positives Delta: Der Call bewegt sich mit dem Basiswert
Beispiel 1: Die Aktie steigt um 1 EUR. Die Option würde um 0,50 EUR (=25%) mitsteigen.
Merke: Die Aktie steigt um 1% (auf 101 EUR) & die Option steigt um 25% (auf 2,50 EUR)!
Beispiel 2: Die Aktie fällt um 1 EUR. Die Option würde um 0,50 EUR (=25%) mitfallen.
Merke: Die Aktie fällt um 1% (auf 99 EUR) & die Option fällt um 25% (auf 1,50 EUR)!
Als Call Käufer (=Long Call) gewinnst du in Beispiel 1 (Kursanstieg) und verlierst in Beispiel 2 (Kursverlust).
- Long Put = Negatives Delta: Der Put bewegt sich entgegen dem Basiswert
Beispiel 1: Die Aktie steigt um 1 EUR. Die Option würde um 0,50 EUR (=25%) fallen.
Merke: Die Aktie steigt um 1% (auf 101 EUR) & die Option fällt um 25% (auf 1,50 EUR)!
Beispiel 2: Die Aktie fällt um 1 EUR. Die Option würde um 0,50 EUR (=25%) steigen.
Merke: Die Aktie fällt um 1% (auf 99 EUR) & die Option steigt um 25% (auf 2,50 EUR)!
Als Put Käufer (=Long Put) verlierst du in Beispiel 1 (Kursanstieg) und gewinnst in Beispiel 2 (Kursverlust).
Soweit klar, oder?
Wiederholen wir das Beispiel nun mit einer Aktie im Wert von 100 EUR und einer Option dazu im Wert von 2 EUR und dem Delta von 0,25 (25%), treten jetzt aber als Verkäufer der Option bzw. als Stillhalter in Aktion.
- Short Call = Negatives Delta: Der Call bewegt sich mit dem Basiswert
Beispiel 1: Die Aktie steigt um 1 EUR. Die Option würde um 0,50 EUR (=25%) mitsteigen.
Merke: Die Aktie steigt um 1% (auf 101 EUR) & die Option steigt um 25% (auf 2,50 EUR)!
Beispiel 2: Die Aktie fällt um 1 EUR. Die Option würde um 0,50 EUR (=25%) mitfallen.
Merke: Die Aktie fällt um 1% (auf 99 EUR) & die Option fällt um 25% (auf 1,50 EUR)!
Das ist bis hierher absolut identisch mit dem Szenario oben als Käufer eines Calls. Jedoch kehrt sich das Vorzeichen von Delta für dich als Verkäufer bzw. Stillhalter um und deswegen gilt nun:
Als Call Verkäufer (=Short Call) verlierst du in Beispiel 1 (Kursanstieg) und gewinnst in Beispiel 2 (Kursverlust).
- Short Put = Positives Delta: Der Put bewegt sich entgegen dem Basiswert
Beispiel 1: Die Aktie steigt um 1 EUR. Die Option würde um 0,50 EUR (=25%) fallen.
Merke: Die Aktie steigt um 1% (auf 101 EUR) & die Option fällt um 25% (auf 1,50 EUR)!
Beispiel 2: Die Aktie fällt um 1 EUR. Die Option würde um 0,50 EUR (=25%) steigen.
Merke: Die Aktie fällt um 1% (auf 99 EUR) & die Option steigt um 25% (auf 2,50 EUR)!
Auch das ist bis hierher absolut identisch mit dem Szenario oben als Käufer eines Puts. Jedoch kehrt sich das Vorzeichen von Delta für dich als Verkäufer bzw. Stillhalter natürlich wieder um und deswegen gilt nun:
Als Put Verkäufer (=Short Put) gewinnst du in Beispiel 1 (Kursanstieg) und verlierst in Beispiel 2 (Kursverlust).
Anmerkung: Diese Beispiele sind rein theoretisch und unter der Annahme, dass keine anderen Faktoren verändernd einwirken. Man nennt dies auch ceteris paribus (unter gleichen Bedingungen). In der Praxis ist das so natürlich nie der Fall, dient hier aber der Veranschaulichung der Funktion von Delta und auch bei allen weiteren Beispielen bei den anderen Griechen, die noch folgen werden.
Bei der ganzen Geschichte rund um Delta handelt es sich leider nicht um eine simple lineare Funktion. Das wäre ja auch zu einfach.
Da ich euch wie versprochen nicht mit Formeln langweilen möchte, hier einmal nur zur Veranschaulichung der Verlauf von Delta am Beispiel von einem Long Call & Long Put:
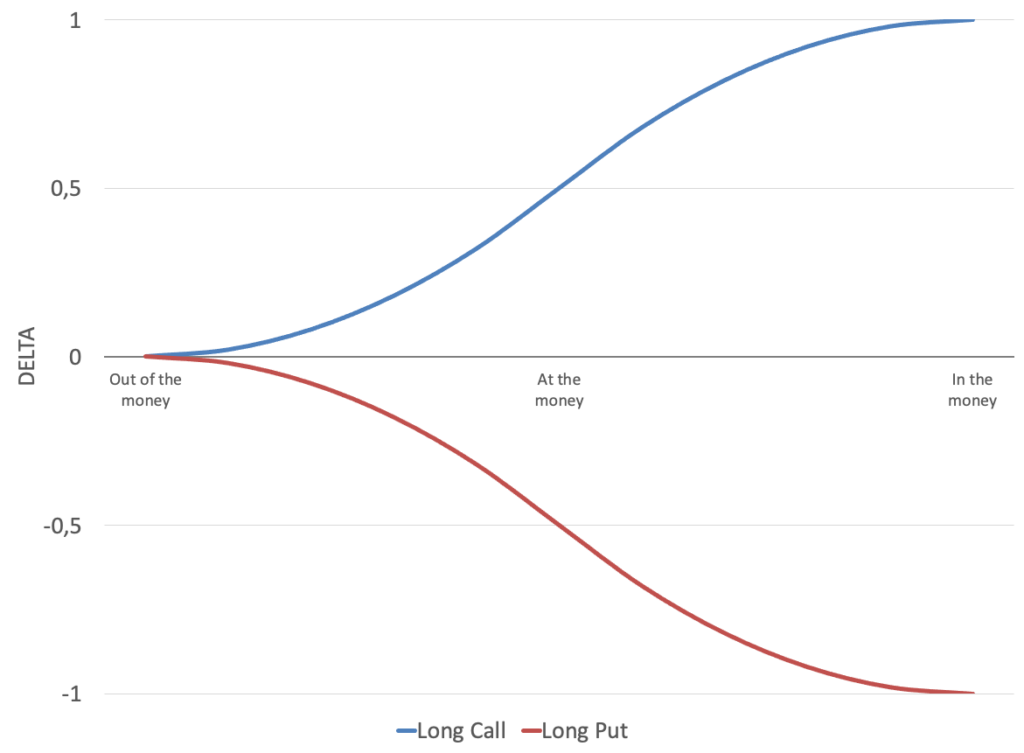
Was bedeutet das jetzt aber in der Praxis und wo hilft uns das?
Im Grunde zeigt das Delta somit die Empfindlichkeit des Optionspreises auf die Veränderung des Aktienkurses auf und man kann damit erkennen, ob ein Optionspreis eher stärker oder eher schwächer mit dem Kurs des Basiswerts mitgehen wird.
Oder umgekehrt und kürzer: Das Delta beschreibt den Einfluss der Kursänderung auf den Optionspreis!
Desweiteren kann man das Delta auch dafür nutzen, um eine grobe Einschätzung zu erlangen, wie wahrscheinlich es ist, dass meine Option zum Verfallstag wertlos verfällt oder nicht. Ein Delta von zum Beispiel 0,2 (20%) sagt grob aus, dass mit einer Wahrscheinlichkeit von ca. 20% die Option am Verfallstag im Geld (in the money) sein wird.
Je nachdem, ob man nun einen Call/Put gekauft oder verkauft hat, ist diese Zahl dann unterschiedlich zu bewerten. Für meine geliebten Cash Secured Puts bedeutet es in diesem Beispiel, dass mit einer Wahrscheinlichkeit von ca. 80% (100%-20%=80%) diese wertlos verfallen werden.
Wenn ich also 2 Optionen vor mir habe, die ich evtl. gern zwecks Prämieneinnahmen verkaufen möchte und kann mich nicht entscheiden, dann könnte man anhand des Delta zumindest schauen, welche Option die (zum aktuellen Zeitpunkt) besseren Chancen hat, wertlos zu verfallen.
Als Stillhalter wollen wir möglichst die höchste Prämie (Rendite) mit dem niedrigsten Delta (Risiko)!
Das Ganze ist nur ein grobes Modell, reicht aber, um die Richtung abschätzen zu können, in die es laufen wird. Allein deswegen finde ich, dass Delta vielleicht sogar der wichtigste Paramater unter den Griechen ist.
Das Gamma

Definition: Das Gamma einer Option gibt an, wie stark sich deren Delta ändert, wenn sich der Kurs des Basiswerts um eine Einheit ändert. Mathematisch ist das Gamma die zweite Ableitung des Optionspreises nach dem Preis des Basiswertes.
Gerade hatten wir das Delta näher beleuchtet und wie sich eine Option im Verhältnis zum Basispreis entwickelt. Leider tut sie das nicht linear, sondern das Delta passt sich nach jeder Veränderung des Basiswerts neu an. Das Gamma drückt diese Veränderung als eine Art Empfindlichkeit aus.
Folgende (vereinfachte) Übersicht dazu:
- Long Call = Positives Gamma
- Basiswert steigt um 1 -> Altes Delta + Gamma = Neues Delta -> Optionspreis steigt
- Basiwert fällt um 1 -> Altes Delta – Gamme = Neues Delta -> Optionspreis fällt
- Long Put = Positives Gamma
- Basiswert steigt um 1 -> Altes Delta – Gamma = Neues Delta -> Optionspreis fällt
- Basiswert fällt um 1 -> Altes Delta + Gamma = Neues Delta -> Optionspreis steigt
Bei einem Short Call oder Short Put ist das Gamma logischerweise dann immer negativ.
Dabei gelten folgende Grundsätze:
- Das maximale Gamma hat eine Option immer dann, wenn sie am Geld (at the money) notiert.
- Je weiter eine Option aus dem Geld (out of the money) oder im Geld (in the money) notiert, desto kleiner ist das Gamma.
Anmerkung: Die Zeit bis zum Verfallstag spielt hier eigentlich auch noch eine größere Rolle, aber das würde das Thema jetzt zu sehr aufblasen und außerdem kommen wir beim Theta noch darauf zu sprechen. Man kann sich aber jetzt schonmal merken, je näher am Geld und je näher am Verfallstag, desto höher die Empfindlichkeit (Stichwort: Es geht um alles!) der Option und damit auch das Gamma.
Ein hohes Gamma bedeutet in dem Zusammenhang also grundsätzlich, dass das Delta bei Änderungen sehr empfindlich reagiert und es einen größeren Einfluss auf den zukünftigen theoretischen Wert von Delta hat.
Ein Beispiel zur Veranschaulichung.
Angenommen ein Call auf eine Aktie hat ein Gamma von 0,05 und ein Delta von 0,6 (60%). Wenn der Basispreis um 1 Euro steigt, steigt auch das neue theoretische Delta für diese Option auf 0,65 (65%). Wenn der Basispreis dagegen um 1 Euro fällt, fällt auch das neue theoretische Delta auf 0,45 (45%).
Zur Verbildlichung von Gamma hier noch ein Diagramm eines Long Calls inkl. des Deltas aus der Abbildung oben:
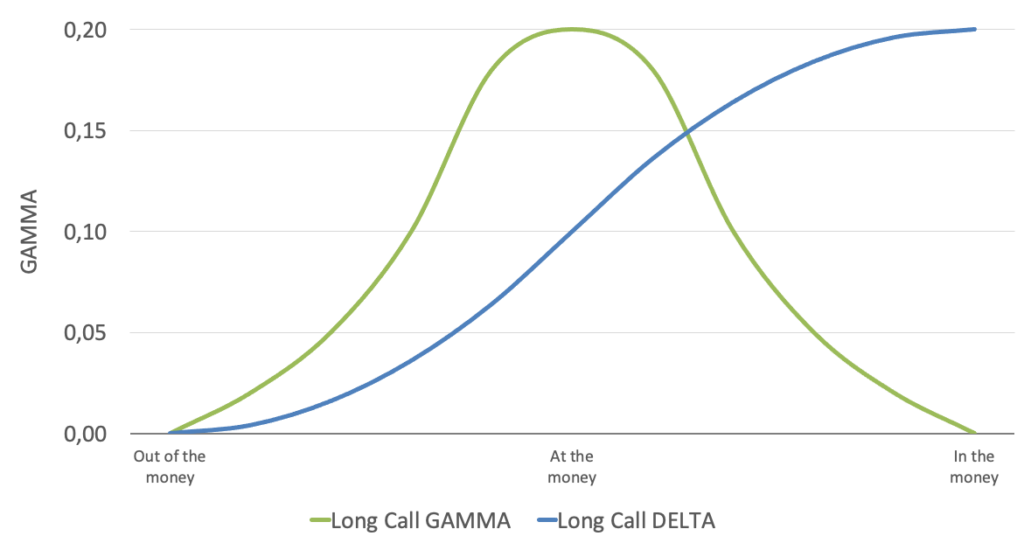
Das Omega

Definition: Das Omega einer Option gibt an, um wieviel Prozent sich der Optionspreis bewegt, wenn sich der Basiswert um 1% bewegt. Omega wird daher auch effektiver Hebel genannt.
Streng genommen gehört das Omega gar nicht zu den Optionsgriechen. Da es aber ein griechischer Buchstabe ist und durchaus eine wertvolle Information zum Optionspreis liefern kann, erwähne ich es hier ganz kurz.
Auf den ersten Blick erscheint Omega mit dem Delta identisch. Und in der Tat sind sie sich sehr ähnlich, unterscheiden sich jedoch in dem Punkt, dass das Delta die Veränderung des Basiswerts immer auf eine Geldeinheit bezieht, also +1 EUR oder -1 EUR, das Omega dagegen den effektiven Hebel in Prozent wiedergibt.
Das macht es um einiges einfacher, mal schnell die Auswirkungen der Veränderung im Basiswert auf den Optionspreis zu prüfen.
Ein Beispiel zur Veranschaulichung.
Ein Call mit einem Omega von 30 verstärkt die Bewegung des Basiswerts um den Faktor 30. Steigt der Basiwert zum Beispiel um 2%, dann steigt der Call um 60%. Fällt der Basiswert dagegen um 3%, dann fällt der Call um 90%. Faktor 30 eben.
Agressive Zocker können diese Information zum Beispiel nutzen, um auf steigende Aktienkurse zu spekulieren. Sie kaufen sich einen Call weit aus dem Geld (out of the money) mit einem möglichst hohem Omega und hoffen, dass der Basiswert steigt. Das ist natürlich deswegen besonders riskant, weil ein hohes Omega in beide Richtungen wirkt und der Basispreis zusätzlich einen weiteren Weg hat, als wenn man die Option näher am Geld (at the money) kaufen würde.
Als Stillhalter interessieren mich solche Strategien zum Glück nur deswegen, weil ich ggf. an diese Leute Optionen verkaufen könnte. Leider fallen deren Basiswerte (Stichwort hohes Momentum) eher selten in mein Beuteschema.
Der Vollständigkeitshalber muss noch gesagt werden, dass das Omega immer dasselbe Vorzeichen wie das Delta hat und das auch das Omega nicht konstant ist und sich bei jeder Änderung des Basiwerts verändert.
Das Theta

Definition: Das Theta einer Option gibt an, wie stark sich der theoretische Wert einer Option ändert, wenn sich die Restlaufzeit um einen Tag verkürzt. Mathematisch ist das Theta die erste partielle Ableitung der Optionspreisfunktion nach der Zeit und wird manchmal auch als Zeit-Delta bezeichnet.
Okay. Theta hat also etwas mit dem so wichtigen Zeitwert einer Option zu tun. Und zwar drückt es aus, wie stark eine Option ihren Zeitwert verliert, wenn ein weiterer Tag bis zum Verfallstag vergangen ist.
Leider ist auch hier das Problem, dass diese Funktion nicht liniear ist und man deswegen nur schwer vorab genau bestimmen kann, wie sich der Zeitwertverlust über die Laufzeit wirklich entwickeln wird.
Zur Veranschaulichung hier ein typischer Verlauf für den Zeitwert einer Option:
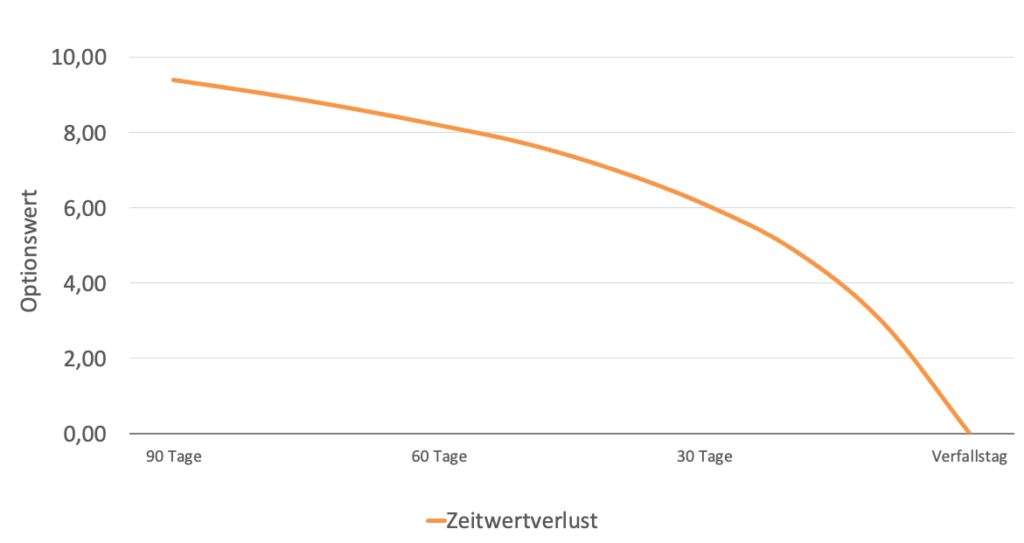
Anhand des Diagramms kann man erkennen:
- Der Zeitwert nimmt stetig ab und nie zu.
- Das Theta für Long Calls und Long Puts ist deswegen immer negativ.
- Das Theta wird mit der Zeit immer stärker negativ und beschleunigt sich.
Letzterer Punkt ist nicht ganz korrekt, um genau zu sein. Optionen, die weit im Geld (in the money) notieren, haben neben dem Zeitwert auch noch einen großen inneren Wert. Hier verläuft das Theta eher linear, solange der innere Werte signifikant ist. Eine Erklärung, warum das so ist, würde an dieser Stelle leider zu weit führen.
Wir merken uns aber, dass das Theta bei Optionen die am Geld (at the money) und besonders bei Optionen die aus dem Geld (out of the money) notieren, denn diese bestehen nur noch aus Zeitwert, unser bester Freund als Stillhalter ist. Denn je näher wir dem Verfallstag kommen, desto stärker ist der Zeitwertverlust und die Option verbilligt sich Tag für Tag merkbar.
Deswegen ist es in der Regel lukrativer als Stillhalter, der am Zeitwertverlust verdienen möchte, dass man vorzugsweise sehr kurzlaufende Optionen verkauft. Allein aus diesem Grund beschränke ich mich bei meiner Strategie auf Optionen mit einer Laufzeit von maximal 45 Tagen, besser 30 Tage oder weniger.
Als Faustregel kann man sich merken, dass bei einem Theta von zum Beispiel -0,1 der Basiswert am nächsten Tag um 0,10 EUR sinken wird. In der Praxis sinkt der Wert zwar schon über den gesamten Tagesverlauf, aber die größte Veränderung wird man immer zwischen dem Schluß- und dem darauffolgenden Eröffnungskurs haben.
Das Vega

Definition: Das Vega einer Option gibt an, um wieviel Prozent sich der Optionspreis ändert, wenn sich die implizierte Volatilität um 1% erhöht.
Huch! Vega? Ein Grieche, der gar kein griechischer Buchstabe ist? Wieso das denn?
Ehrlich? Ich habe keine Ahnung!
Vielleicht weil Volatilität mit V anfängt und es leider kein V im herkömmlichen Sinne im griechischen Alphabet gibt?
Um die Verwirrung komplett zu machen, als Symbol wird in der Regel das Zeichen „v“ vom griechische Buchstaben „Ny“ hergenommen.
Das muss man nicht verstehen, oder?
Anmerkung: In manchen mathematischen Abhandlungen zum Optionspreismodell wird statt Vega dann doch ein griechischer Buchstabe verwendet, nämlich das Lambda oder das Kappa. Scheinbar hat man sich bis heute nicht auf eine saubere Regelung einigen können. Pfff … Wissenschaftler!
Davon abgesehen ist Vega jedoch durchaus spannend, denn die Volatilität (sowohl die hier angesprochene implizierte Volatilität, als auch die historische Volatilität) spielt beim Optionshandel in der Regel eine große Rolle.
Ein Vega von 0,1 würde bei einer 20 EUR Option bedeuten, dass beim Anstieg der implizierten Volatilität des Basiswerts um 1%, diese Option auf 22 EUR steigen würde. Ein Anstieg der Volatilität führt somit in der Regel zu einem Anstieg des Optionspreises.
Folgende (vereinfachte) Übersicht dazu:
- Long Call = Positives Vega
- Vola des Basiswerts steigt um 1% -> Optionspreis + Vega = Neuer Optionspreis -> Preis steigt
- Vola des Basiwerts fällt um 1% -> Optionspreis – Vega = Neuer Optionspreis -> Preis fällt
- Long Put = Positives Vega
- Vola des Basiswerts steigt um 1% -> Optionspreis + Vega = Neuer Optionspreis -> Preis steigt
- Vola des Basiswerts fällt um 1% -> Optionspreis + Vega = Neuer Optionspreis -> Preis fällt
Man sieht, das Vega ist bei Long Optionen immer positiv und als Käufer profitiert man von einem Anstieg der implizierten Volatilität. Dagegen ist das Vega bei Short Optionen immer negativ und als Verkäufer bzw. Stillhalter profitiert man somit vom Rückgang der implizierten Volatilität.
Als Stillhalter wollen wir also möglichst unsere Optionen bei einer hohen implizierten Volatilität verkaufen und sie später bei einer Normalisierung günstiger zurückkaufen. Das funktioniert zum Beispiel immer sehr gut um den Zeitpunkt der sogenannten Earnings (Quartalszahlen) herum oder wenn ein spezielles Ereignis den Markt oder Teile des Marktes stark nach oben oder unten schickt.
Wie auch schon beim Gamma beobachtet, ist das Vega bei Optionen die am Geld (at the money) notieren am höchsten und nimmt ab je weiter eine Option entweder im Geld (in the money) oder aus dem Geld (out of the money) notiert.
Zur Veranschaulichung hier ein typischer Verlauf für das Vega einer Option:
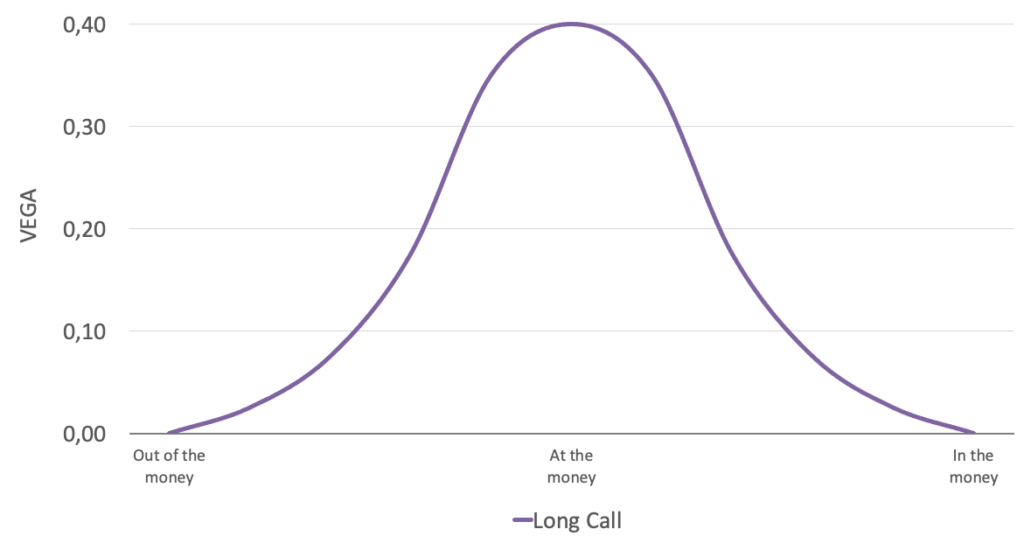
Zusätzlich nimmt das Vega über die Laufzeit immer weiter ab. Das bedeutet, je länger eine Option noch läuft, umso empfindlicher reagiert sie auf den Anstieg oder den Abfall der implizierten Volatilität. Oder andersrum ausgedrückt, je kürzer die Restlaufzeit, desto geringer die Auswirkungen der Volatilität auf den Optionspreis.
Das Rho

Definition: Das Rho ist die erste partielle Ableitung der Optionspreisfunktion nach dem Zins und es drückt aus, wie stark sich der Wert der Option ändert, wenn sich der risikofreie Zinssatz am Markt um 1% (100 Basispunkte) ändert.
Ich hoffe jetzt niemanden zu enttäuschen, wenn ich sage, dass ich nicht näher auf die Funktion von Rho eingehen werde, aber ich wollte es zumindest erwähnt haben. Wobei, ein kleines Beispiel kann ich ja gern kurz darstellen.
Nehmen wir eine Option zum Preis von 10 EUR und 6 Monate Laufzeit. Der Marktzins für 6 Monate liegt bei exemplarischen 1% p.a. und das Rho beträgt 0,05. Wenn sich nun der Marktzins auf 2% p.a. erhöht, dann erhöht sich der Optionspreis um 0,05 EUR.
Dagegen würde in dem Beispiel eine Zinsreduzierung um 0,5% p.a. den Optionspreis um 0,025 EUR (-0,5 x 0,05 = 0,025) verringern.
Der Einfluss vom Zins auf (vorallem kurzlaufende) Optionen, mal ganz davon abgesehen, dass es aktuell gar keine Zinsen gibt, ist sehr gering. Außerdem korreliert Rho positiv mit Vega und so kann man den Einfluss bei Bedarf auch darüber abbilden bzw. ablesen. Je niedriger der Einfluss von Vega, desto niedriger auch der eh schon geringe Einfluss von Rho.
Wir können das Thema Rho ja gern noch einmal hervorholen, wenn die Notenbanken wieder so etwas wie einen Zins einführen. Deal?
Die Griechen in der TWS
Fragt ihr euch jetzt, wo man die aktuellsten Daten bzgl. der Griechen für die Optionen herbekommen kann?
Für alle Nutzer der TWS (Trader Workstation) kann man diese Information ganz einfach als weitere Spalten im Portfolio, in den Watchlisten oder den Optionsketten (Option Chain) hinzufügen.
Klickt dazu einfach auf die Spaltenüberschrift, wählt dann Spalte einfügen (Insert Column) und wählt dann Greeks aus. Dort findet ihr die Informationen zu den 4 wichtigsten Griechen, nämlich Delta, Gamma, Theta und Vega.
Hier ein Screenshot aus meinem aktuellen Depot:

Andere frei verfügbare Quellen sind mir nicht bekannt. Wahrscheinlich aber vorallem deswegen, weil ich nie danach gesucht habe. Wer eine kennt, kann diese Info ja gern mal in den Kommentaren teilen. Danke!
Mein Optionskonto bei Estably
Wer übrigens mit dem Optionshandel beginnen möchte und noch nach einem günstigen Broker dafür sucht, dem kann ich Estably* ans Herz legen. Ich selbst habe mein Depot für den Optionshandel seit nunmehr fast 5 Jahren dort und bin sehr zufrieden.

Estably fungiert hier als sogenannter Reseller für Interactive Brokers (IB) und du bekommst natürlich Zugriff auf alle professionellen Tools, wie zum Beispiel die gerade erwähnte TWS, die dort verfügbar sind. Plus du hast bei Bedarf Zugriff auf nette und kompetente deutsche Ansprechpartner, falls mal eine Frage oder ein Problem geklärt werden muss.
Wenn du dich mit meinem GS-Code „Mission-Cashflow“ anmeldest, bekommst du zusätzlich noch vergünstigte Konditionen beim Optionshandel. 1,80 EUR für DE-Optionen und 3,00 USD für US-Optionen.
Du kannst aber auch gern erstmal nur ein Demo-Konto eröffnen und mit Papiergeld dich versuchen. Wie du möchtest. Auch diese Möglichkeit hast du bei Estably.
Schlussbemerkung & Fazit
Okay, damit hätten wir es. Ziemlich interessant, oder?
Jedoch wirken alle diese genannten Faktoren gleichzeitig auf den Optionspreis ein und deswegen ist die Geschichte am Ende ziemlich kompliziert. Ich komme die meiste Zeit auch ohne dieses Wissen aus und kann trotzdem sehr erfreuliche Ergebnisse mit meinem Optionshandel vorweisen.
Lustig wird das Ganze dann, wenn man darüber hinaus weiß, dass selbst das bereits weiter oben genannte Black-Schole-Modell, übrigens Nobelpreis prämiert, mittlerweile von einigen Finanzmathematikern angezweifelt und als nicht komplett bezeichnet wird. Hintergrund ist hier, dass es von einer Normalverteilung der Wertveränderungen ausgeht, was in der Praxis so aber offensichtlich nicht der Fall ist.
Egal wie man das nun alles bewertet, es ist nie verkehrt darüber Bescheid zu wissen und ab und zu mal zumindest einzelne Parameter zur Bewertung zu Rate ziehen zu können, kann durchaus bei der Auswahl der richtigen Option helfen.
Ich hoffe, ich konnte das Thema halbwegs einfach vermitteln und freue mich auf eure Fragen, Kommentare und ggf. Anregungen für weitere Artikel rund um den Optionshandel.
Danke fürs Lesen und wenn dir der Artikel gefallen hat, hinterlasse mir einen Kommentar und teile ihn mit deinen Freunden auf Social Media oder in deinem Lieblingsforum. Das würde mir sehr viel bedeuten. Vielen Dank!




Hallo Ingo,
schöne Zusammenstellung.
Ich denke man sollte die Angaben kennen. Insbesondere die Delta/Gamma-Kurven um den Basispreis-
Dazu die (implizierte)Vola und die Zeitwertkurve.
Beim aktiven Longoptionshandel glaube ich ist es detaillierter notwendig, da man Hebel ausnutzt.
So wie wir CashSecuredPut oder Covered Calls schreiben reicht das grundsätzliche Verständnis um Basispreis und Laufzeit zu bestimmen.
Ich schaue auch auf CBOE direkt nach. Sind halt zeitverzögert, solange man nicht bezahlen möchte.
https://www.cboe.com/delayed_quotes/brx/quote_table. Geht man auf einen Preis erhält man die dazugehörigen Details der Option bzw. auch die Voladaten des Basiswertes.
Viele Grüße und ein schönes Wochenende,
Torsten
Hi Torsten!
Danke fürs Vorbeischauen.
Du hast absolut Recht damit, dass es ggf. interessanter ist für die Long Trader. Also die, die Optionen kaufen und auf einen bestimmten Ausgang spekulieren.
Für Stillhalter ist es eher nicht so wichtig und wie im Artikel auch gesagt, ich komme die meiste Zeit ohne diese Infos aus.
Danke für den Link!
CU Ingo.
Moin Ingo,
ich weiß schon, warum ich Interessierten immer wieder deine Options-Serie weiterempfehle!
Denn auch mit dem vorliegenden Teil der Artikelreihe hast du mal wieder sehr gute Arbeit geleistet – auch wenn ich dir recht geben muss:
Ob man das alles bei jener Form des Optionshandels, den wir betreiben, wirklich berücksichtigen muss, sei mal dahin gestellt…
Nichtsdestotrotz klasse Arbeit!
Besten Gruß und ein schönes Wochenende,
David
Hi David!
Danke fürs Vorbeischauen.
Es freut mich sehr, wenn du mein Optionshandel ABC empfehlen kannst und es auch tust. Danke sehr!
CU Ingo.
Hi Ingo,
ich schreib ja eher selten hier. Nur wenn mir ein interessanter Titel über den Weg lief (z.B. letztes Jahr mal Omnicon oder zuletzt Fresenius).
Gerade bei Fresenius hatte ich ja erwähnt, dass du deinen „regelmäßigen Spaß“ beim Optionshandel hast und damit wahrscheinlich mehr Ruhe im Dividendendepot. Nun ja, ich etwas drüber nachgedacht und es als Anlass genommen deine Artikel zur Optionsstrategie mal durchzulesen. Und ehrlich: Chapeau. Wirklich gut beschrieben und die Balance zwischen Information und Lesemotivation getroffen.
Ich hab mir jedenfalls mit deinem Link ein Konto bei Banx eröffnet und versuche mich mal in die Optionsthematik einzutesten. Sehe das nämlich ähnlich wie du: Bisschen Theorie ist wichtig, aber dann muss auch schnell die Praxis und damit die Erfahrung kommen.
Ich bin mal gespannt, wie das läuft und ob man tatsächlich so 1-1,5 % pro Monat erwirtschaften kann. Wie verwaltest du den excelseitig dein Optionsdepot eigentlich?
Viele Grüße,
Christian
Hi Christian!
Danke fürs Vorbeischauen und freut mich, wenn ich dich für das Thema Optionen begeistern konnte.
Probier es einfach aus. Mit der Zeit wird sich schon zeigen, ob es etwas für dich ist oder nicht.
Mein Depot verwalte ich zum einen direkt mit dem, was mir Banx/IB anbietet und dann mit einem von mir manuell gepflegten Exceltemplate. Letzteres auch deswegen, damit ich so eine Art „Tagebuch“ aller meiner Trades immer vor Augen habe. Finde ich wichtig, da man so das Gelernte nicht wieder vergisst.
Viel Erfolg bei deinen ersten Trades!
CU Ingo.
Hi Ingo,
was die Verwaltung anbetrifft, hab ic bei Banx noch nicht so eine theoretische jährliche Rendite finden können. Deswegen hab ich ein einfaches Excel zusammengestellt, um diese Zahl als ein Indikator zu nehmen.
Werden bei IAB eigentlch nur eine Art von Optionen (amerikanisch, europäisch gehandelt)? Falls beide gehandelt werden: Kansst du einen Tipp geben wo ich die Info finde was was ist?
Besten Dank,
Christian
Hi Christian!
Alle Performancekennzahlen findest du bei Banx/IB in der Kontoverwaltung. Da kannst du jeden Zeitraum filtern, den du dir ansehen möchtest und es gibt TWR (time weighted return) und MWR (money weighted return) zur Auswahl. Das ist in meine Augen alles, was man so braucht.
In der TWS habe ich noch keine Möglichkeiten gefunden mir anzeigen zu lassen, ob eine Option amerikanisch oder europäisch ist. Grundsätzlich gilt aber, an europäischen Börsen werden europäische Optionen gehandelt und an amerikanischen Börsen halt amerikanische. Irgendwie auch logisch, oder?
Wäre dann nur noch die Frage, was ist im Rest der Welt (Hong Kong etc.). Ich vermute amerikanischer Typ, aber sicher bin ich mir nicht.
CU Ingo.
Hi Ingo, besten Dank für die Rückmeldung. Zum Thema amerikanisch oder europäisch hab ich in der Zwischenzeit auch bisschen recherchiert. Das sind wohl meistens amerikanische Typen, auch wenn sie über die eurex gehandelt werden. Siehe Beispiel Fresenius.
https://www.eurex.com/ex-en/markets/equ/opt/Fresenius-951596
Viele Grüße
Hi Christian!
Danke fürs Teilen.
Lt. dem Link sind aber DE, CH, FR, FI und NL Optionen eurpäischen Typs oder verwechsle ich da etwas?
CU Ingo.
Ich glaub du hast recht. Da hatte ich etwas falsch gelesen.
FRE sind amerikanische. Unter Spezifikationen steht unter Ausführungszeit, dass sie an jedem Börsentag ausgeübt werden dürfen.
An der Eurex gibt es zum Teil beide. Für Daimler gibt es DAI (amerikanische) und DAIE (europäische) Optionen an der Eurex. Zumindest sollte man nachschauen, um welche Art es sich handelt.
@Torsten: Danke für die Rückmeldung. Jetzt muss ich nochmal nachhaken. Wo genau hast du die Info her? Findest du die Auch beim IB? Oder auf der Eurex-Seite. Dort steht in den Spezifikationen das DE14 europäische sind. Aber das DE14 finde ich nirgends wieder.
Europäische Ausübung ist die Ausnahme.
https://www.eurex.com/resource/blob/1256/dad7a74a443a30e1febbd60ce3f61490/data/presentation_eurex-equity-options.pdf
In der Präsentation sieht man, dass es nur 36 europäische Aktienoptionen gibt. Auf der Eurexseite steht dies als Zusatz dann beim Namen und das Kürzel um ein E ergänzt.
Sehr interessant. Ich hab gleich mal nachgesehen. Da steht dann bei ABB zum Beispiel wirklich ABBE und extra [european] dahinter.
https://www.eurex.com/ex-en/markets/equ/opt/ABB-european–950458
Wieder etwas gelernt. Sehr gut! 🙂